1.什么是对偶问题?
在线性规划的早期发展中最重要的发现就是对偶问题,即每一个线性规划问题(称为原始问题)都有一个与它对应的对偶线性规划问题(称为对偶问题)。
2.优化问题
2.1 无约束的优化问题
$\mathop{min}f(x)$
其中,$x=(x_{1},x_{2})$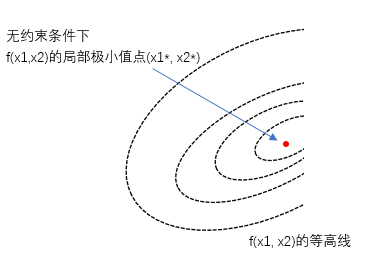
注意在图里画了等高线。此时$f(x)$ 在局部极小值点 $x^* =(x_{1}^*,x_{2}^*) $ 处的梯度必然为0,比较容易理解。这个梯度为零的条件是局部极小值点的必要条件。这样,优化问题的求解变成了对该必要条件解方程组。
2.2 带等式约束的优化问题
$\mathop{min}f(x)$
s.t.
$h(x)=0$
与无约束的问题不同。我们所要求的极小值点被限制在曲线$h(x) = 0$上,我们将${x|h(x)=0}$称为可行域, 解只能在这个可行域里取。如下图所示,曲线$h(x) = 0$ (黑色实曲线)经过无约束极小值点(黑点)附近。那么满足约束的极小值点应该与黑点尽可能近。我们将$f(x)$ 的等高线不断放大,直到与曲线 $h(x) = 0$ 相切,切点即为所求。相切是关键,是极小值点的必要条件。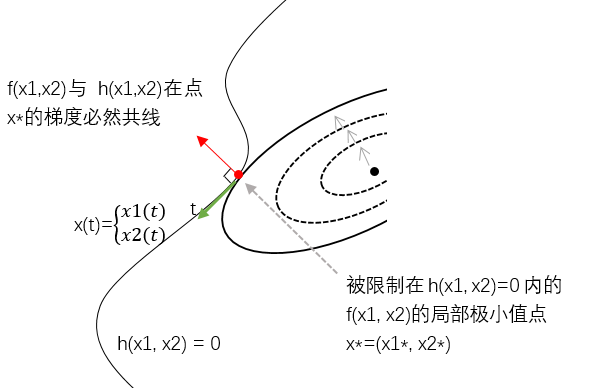

令其偏导为0,正好就得到拉格朗日条件。
如此,带等式约束的优化问题转化为了无约束的优化问题,只需要对拉格朗日条件解方程组即可。这里λ就是拉格朗日乘子,有多少个等式约束就有多少个拉格朗日乘子。
2.3 带不等式约束的优化问题
$\mathop{min} f(x)$
$ s.t $
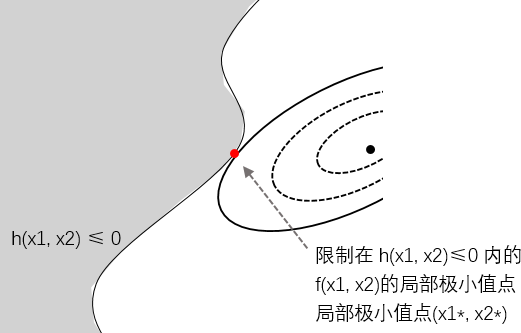
$h(x) \leq 0 $
当只有一个不等式起作用时, 如我们把问题2里的等式约束$h(x) = 0$ 改为 $h(x) \leq 0$, 如下图所示,可行域变成了阴影部分,最小值点还是切点,情况和问题2完全一样,只需要把不等号当做等号去求解即可。