1. Error的来源
Error 的主要有两个来源,分别是 bias 和 variance。
1.1. bias 和 variance
Error = Bias + Variance
Error反映的是整个模型的准确度,Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
举一个例子,一次打靶实验,目标是为了打到10环,但是实际上只打到了7环,那么这里面的Error就是3。具体分析打到7环的原因,可能有两方面:一是瞄准出了问题,比如实际上射击瞄准的是9环而不是10环;二是枪本身的稳定性有问题,虽然瞄准的是9环,但是只打到了7环。那么在上面一次射击实验中,Bias就是1,反应的是模型期望与真实目标的差距,而在这次试验中,由于Variance所带来的误差就是2,即虽然瞄准的是9环,但由于本身模型缺乏稳定性,造成了实际结果与模型期望之间的差距。
知乎链接:机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系?
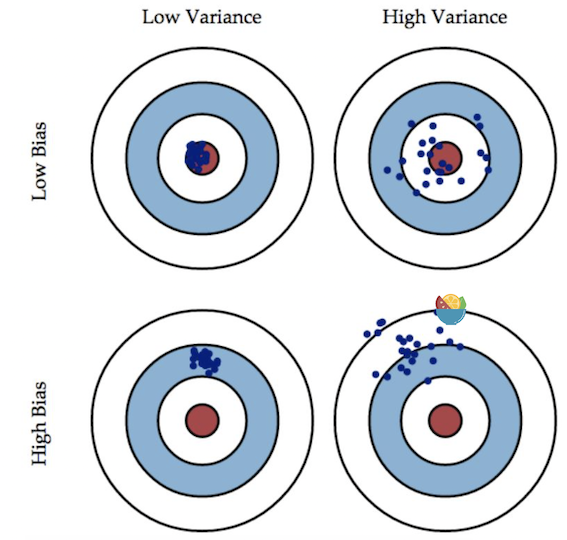
在一个实际系统中,Bias与Variance往往是不能兼得的。如果要降低模型的Bias,就一定程度上会提高模型的Variance,反之亦然。造成这种现象的根本原因是,我们总是希望试图用有限训练样本去估计无限的真实数据。当我们更加相信这些数据的真实性,而忽视对模型的先验知识,就会尽量保证模型在训练样本上的准确度,这样可以减少模型的Bias。但是,这样学习到的模型,很可能会失去一定的泛化能力,从而造成过拟合,降低模型在真实数据上的表现,增加模型的不确定性。相反,如果更加相信我们对于模型的先验知识,在学习模型的过程中对模型增加更多的限制,就可以降低模型的variance,提高模型的稳定性,但也会使模型的Bias增大。Bias与Variance两者之间的trade-off是机器学习的基本主题之一。
1.2. 考虑不同模型的方差
用比较简单的模型,方差是比较小的(就像射击的时候每次的时候,每次射击的设置都集中在一个比较小的区域内)。如果用了复杂的模型,方差就很大,散布比较开。
这也是因为简单的模型受到不同训练集的影响是比较小的。
1.3. 考虑不同模型的偏差
简单模型的偏差比较大,variance比较小。而复杂的模型,偏差比较小,variance比较大。
直观的解释:简单的模型函数集的space比较小,所以可能space里面就没有包含靶心,肯定射不中。而复杂的模型函数集的space比较大,可能就包含的靶心,只是没有办法找到确切的靶心在哪,但足够多的,就可能得到真正的 $\bar{f}$。
1.3.1. 偏差v.s.方差

简单模型(左边)是偏差比较大造成的误差,这种情况叫做欠拟合,而复杂模型(右边)是方差过大造成的误差,这种情况叫做过拟合。
1.3.2. 过拟合,欠拟合
如果模型没有很好的训练训练集,就是偏差过大,也就是欠拟合 如果模型很好的训练训练集,即再训练集上得到很小的错误,但在测试集上得到大的错误,这意味着模型可能是方差比较大,就是过拟合。 对于欠拟合和过拟合,是用不同的方式来处理的。
1.3.3. 偏差大-欠拟合
此时应该重新设计模型。因为之前的函数集里面可能根本没有包含$f^*$。可以:
1.3.4. 方差大-过拟合
简单粗暴的方法:更多的数据
但是很多时候不一定能做到收集更多的data。可以针对对问题的理解对数据集做调整。比如识别手写数字的时候,偏转角度的数据集不够,那就将正常的数据集左转15度,右转15度,类似这样的处理。
1.4. 交叉验证

图中public的测试集是已有的,private是没有的,不知道的。交叉验证 就是将训练集再分为两部分,一部分作为训练集,一部分作为验证集。用训练集训练模型,然后再验证集上比较,确实出最好的模型之后(比如模型3),再用全部的训练集训练模型3,然后再用public的测试集进行测试,此时一般得到的错误都是大一些的。
上述方法可能会担心将训练集拆分的时候分的效果比较差怎么办,可以用下面的方法。
1.5. N-折交叉验证
将训练集分成N份,比如分成3份。

比如在三份中训练结果Average错误是模型1最好,再用全部训练集训练模型1。
2. 梯度下降(Gradient Descent)
调整学习速率

上图左边黑色为损失函数的曲线,假设从左边最高点开始,如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。如果学习率调整的太小,比如蓝色的线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。如果 学习率调整的有点大,比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
上图右边,对学习率大小对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
自适应学习率(Adaptive Learning Rate)
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率
- 通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
update好几次参数之后呢,比较靠近最低点了,此时减少学习率
比如 $\eta^t =\frac{\eta^t}{\sqrt{t+1}}$,$t$ 是次数。随着次数的增加,$\eta^t$ 减小
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
Adagrad 算法
Adagrad 是什么?
每个参数的学习率都把它除上之前微分的均方根。解释:
普通的梯度下降为:
- $w$ 是一个参数
Adagrad 可以做的更好:
- $\sigma^t$ :之前参数的所有微分的均方根,对于每个参数都是不一样的。
参数的更新过程:
随机梯度下降法
之前的梯度下降:
而随机梯度下降法更快:
损失函数不需要处理训练集所有的数据,选取一个例子 $x^n$
此时不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数$L_n$,就可以快速update 梯度。
Feature Scaling 特征缩放
比如有个函数:
两个输入的分布的范围很不一样,建议把他们的范围缩放,使得不同输入的范围是一样的。

为什么要这样做?
上图左边是 $x_1$ 的scale比 $x_2$ 要小很多,所以当 $w_1$ 和 $w_2$ 做同样的变化时,$w_1$ 对 $y$ 的变化影响是比较小的,$x_2$ 对 $y$ 的变化影响是比较大的。
坐标系中是两个参数的error surface(现在考虑左边蓝色),因为 $w_1$ 对 $y$ 的变化影响比较小,所以 $w_1$ 对损失函数的影响比较小,$w_1$ 对损失函数有比较小的微分,所以 $w_1$ 方向上是比较平滑的。同理 $x_2$ 对 $y$ 的影响比较大,所以 $x_2$ 对损失函数的影响比较大,所以在 $x_2$ 方向有比较尖的峡谷。
上图右边是两个参数scaling比较接近,右边的绿色图就比较接近圆形。
对于左边的情况,上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的,两个方向上需要不同的学习率,同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
缩放的方法非常多,如:
- min-max标准化(min-max normalization)
- log函数转换
- atan函数转换
- z-score标准化—>零均值规范化(zero-mena normalization,此方法比较常用)
- 模糊量化法。
参考 Code
https://github.com/datawhalechina/leeml-notes/tree/master/docs/Homework/HW_1


