西瓜书第4章 决策树
1. 算法原理
决策树是基于树结构对问题进行决策或判定的过程。
决策过程中提出的判定问题(内部节点)是对某个属性的“测试”,每个测试的结果可以导出最终结论(叶节点)或导出进一步判定问题(下一层内部节点,其考虑范围是在上次决策结果的限定范围之内)。
算法核心:选取划分条件(划分属性)。
最终目的:样本划分越“纯”越好。
在网上看到一个例子十分有趣,放在这里正好合适。现想象一位捉急的母亲想要给自己的女娃介绍一个男朋友,于是有了下面的对话:
1 | 女儿:多大年纪了? |
这个女孩的挑剔过程就是一个典型的决策树,即相当于通过年龄、长相、收入和是否公务员将男童鞋分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么使用下图就能很好地表示女孩的决策逻辑(即一颗决策树)。
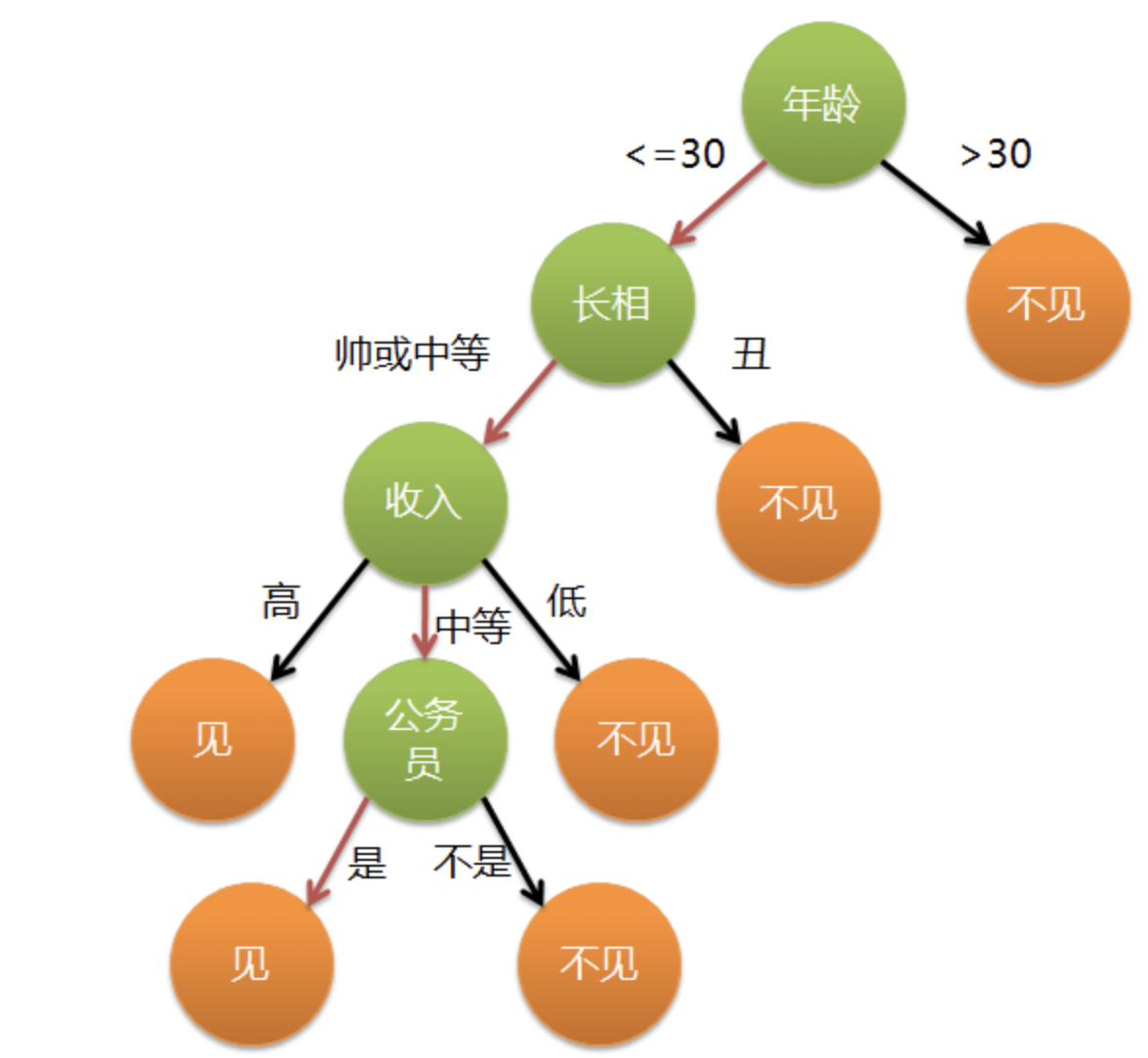
在上图的决策树中,决策过程的每一次判定都是对某一属性的“测试”,决策最终结论则对应最终的判定结果。一般一颗决策树包含:一个根节点、若干个内部节点和若干个叶子节点,易知:
* 每个非叶节点表示一个特征属性测试。
* 每个分支代表这个特征属性在某个值域上的输出。
* 每个叶子节点存放一个类别。
* 每个节点包含的样本集合通过属性测试被划分到子节点中,根节点包含样本全集。
2. 决策树的构造
决策树的构造是一个递归的过程,有三种情形会导致递归返回:
- 当前结点包含的样本全属于同一类别,这时直接将该节点标记为叶节点,并设为相应的类别;
- 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分,这时将该节点标记为叶节点,并将其类别设为该节点所含样本最多的类别;
- 当前结点包含的样本集合为空,不能划分,这时也将该节点标记为叶节点,并将其类别设为父节点中所含样本最多的类别。
算法基本流程伪码

可以看出:决策树学习的关键在于如何选择划分属性,不同的划分属性得出不同的分支结构,从而影响整颗决策树的性能。属性划分的目标是让各个划分出来的子节点尽可能地“纯”,即属于同一类别。因此下面便是介绍量化纯度的具体方法,决策树最常用的算法有三种:ID3,C4.5和CART。
3. ID3算法
ID3算法使用信息增益为准则来选择划分属性,“信息熵”(information entropy)是度量样本结合纯度的常用指标,假定当前样本集合D中第k类样本所占比例为pk,则样本集合D的信息熵定义为:
信息熵值越大越混乱。
假定通过属性划分样本集D,产生了V个分支节点,v表示其中第v个分支节点,易知:分支节点包含的样本数越多,表示该分支节点的影响力越大。故可以计算出划分后相比原始数据集D获得的“信息增益”(information gain)。
信息增益越大,表示使用该属性划分样本集D的效果越好,因此ID3算法在递归过程中,每次选择最大信息增益的属性作为当前的划分属性。
4. C4.5算法
ID3算法存在一个问题,就是偏向于取值数目较多的属性,例如:如果存在一个唯一标识,这样样本集D将会被划分为|D|个分支,每个分支只有一个样本,这样划分后的信息熵为零,十分纯净,但是对分类毫无用处。因此C4.5算法使用了“增益率”(gain ratio)来选择划分属性,来避免这个问题带来的困扰。首先使用ID3算法计算出信息增益高于平均水平的候选属性,接着C4.5计算这些候选属性的增益率,增益率定义为:
其中:
IV(a) 称为属性a的”固有值”。属性a的可能取值数目越多(即越大),则IV(a)的值通常会越大。
C4.5 算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:
先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
5. CART算法
CART是Classification and Regression Tree的简称,这是一种著名的决策树学习算法,分类和回归任务都可用。其生成的决策树为二叉树。
CART决策树使用“基尼指数”(Gini index)来选择划分属性,基尼指数反映的是从样本集D中随机抽取两个样本,其类别标记不一致的概率,因此Gini(D)越小越好,基尼指数定义如下:
任取两个样本不一致的概率,越小表示集合越纯
进而,使用属性α划分后的基尼指数为:
选择基尼指数最小的属性作为最优划分属性:
算法流程
- 对每个属性a的每个可能取值v,将数据集D分为$a=v$和$a \neq v $两部分来计算基尼指数,即:
选择基尼指数最小的属性及其对应取值作为最优划分属性和最优划分点;
重复以上两步,直至满足停止条件。
6. 剪枝处理
剪枝(pruning)是决策树学习算法对付”过拟合”的主要手段。,为了尽可能正确分类训练样本,有时会造成决策树分支过多,以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合。可通过主动去掉一些分支来降低过拟合的风险。
剪枝基本策略包括”预剪枝“(prepruning)和”后剪枝“(post”pruning)。
可以用交叉验证的方法,即预留一部分数据用作”验证集”以进行性 能评估,以判断剪枝是否能带来算法泛化性能的提升。
预剪枝
预剪枝指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
优点
预剪枝使得决策树的很多分支都没有”展开“,可以降低过拟合的风险;
显著减少决策树的训练时间开销和测试时间开销。缺点
有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降,但在其基础上进行的后续划分却有可能导致性能显 著提高;
预剪枝基于”贪心”本质禁止这些分支展开,可能导致欠拟合。
后剪枝
后剪枝先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
根据奥卡姆剃刀准则,剪枝后的模型更好。因此,后剪枝下,决策树算法在验证集精度虽无提高的情况中会进行剪枝。
- 优点
一般情形下,后剪枝决策树的欠拟合风险很小,泛化能往往优于预剪枝决策树; - 缺点
后剪枝过程是在生成完全决策树之后进行的,并且要白底向上对树中的所有非叶结点进行逐一考察,因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。
7. 连续值与缺失值处理
对于连续值的属性,若每个取值作为一个分支则显得不可行,因此需要进行离散化处理,常用的方法为二分法,基本思想为:给定样本集D与连续属性α,二分法试图找到一个划分点t将样本集D在属性α上分为≤t与>t。
- 首先将α的所有取值按升序排列,所有相邻属性的均值作为候选划分点(n-1个,n为α所有的取值数目)。
- 计算每一个划分点划分集合D(即划分为两个分支)后的信息增益。
- 选择最大信息增益的划分点作为最优划分点。
现实中常会遇到不完整的样本,即某些属性值缺失。有时若简单采取剔除,则会造成大量的信息浪费,因此在属性值缺失的情况下需要解决两个问题:(1)如何选择划分属性。(2)给定划分属性,若某样本在该属性上缺失值,如何划分到具体的分支上。假定为样本集中的每一个样本都赋予一个权重,根节点中的权重初始化为1,则定义:
对于(1):通过在样本集D中选取在属性α上没有缺失值的样本子集,计算在该样本子集上的信息增益,最终的信息增益等于该样本子集划分后信息增益乘以样本子集占样本集的比重。即:

对于(2):若该样本子集在属性α上的值缺失,则将该样本以不同的权重(即每个分支所含样本比例)划入到所有分支节点中。该样本在分支节点中的权重变为:
参考代码
Decision Tree(纯Python实现)
决策树iris_data
决策树实现mnist数据集
参考文献
《机器学习》——周志华
【吃瓜教程】《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集


