第一章学习笔记
1、引言
傍晚小街路面上沁出微雨后的湿润,和熙的细风吹来,抬头看看天边的晚霞,嗯,明天又是一个好天气。走到水果摊旁,挑了个根蒂蜷缩、敲起来声音浊响的青绿西瓜,一边满心期待着皮薄肉厚瓢甜的爽落感,一边愉快地想着,这学期狠下了工夫,基础概念弄得清清楚楚,算法作业也是信手拈来,这门课成绩一定差不了!
1.1、机器学习的定义
正如我们根据过去的经验来判断明天的天气,吃货们希望从购买经验中挑选一个好瓜,那能不能让计算机帮助人类来实现这个呢?机器学习正是这样的一门学科,人的“经验”对应计算机中的“数据”,让计算机来学习这些经验数据,生成一个算法模型,在面对新的情况中,计算机便能作出有效的判断,这便是机器学习。
另一本经典教材的作者Mitchell给出了一个形式化的定义,假设:
- P:计算机程序在某任务类T上的性能。
- T:计算机程序希望实现的任务类。
- E:表示经验,即历史的数据集。
若该计算机程序通过利用经验E在任务T上获得了性能P的改善,则称该程序对E进行了学习。
1.2、机器学习的一些基本术语
假设我们收集了一批西瓜的数据,例如:(色泽=青绿;根蒂=蜷缩;敲声=浊响), (色泽=乌黑;根蒂=稍蜷;敲声=沉闷),(色泽=浅自;根蒂=硬挺;敲声=清脆)……每对括号内是一个西瓜的记录,定义:
- 所有记录的集合为:数据集。
- 每一条记录为:一个实例(instance)或样本(sample)。
- 例如:色泽或敲声,单个的特点为特征(feature)或属性(attribute)。
- 对于一条记录,如果在坐标轴上表示,每个西瓜都可以用坐标轴中的一个点表示,一个点也是一个向量,例如(青绿,蜷缩,浊响),即每个西瓜为:一个特征向量(feature vector)。
- 一个样本的特征数为:维数(dimensionality),该西瓜的例子维数为3,当维数非常大时,也就是现在说的“维数灾难”。
计算机程序学习经验数据生成算法模型的过程中,每一条记录称为一个“训练样本”,同时在训练好模型后,我们希望使用新的样本来测试模型的效果,则每一个新的样本称为一个“测试样本”。定义:
所有训练样本的集合为:训练集(trainning set),[特殊]。
- 所有测试样本的集合为:测试集(test set),[一般]。
- 机器学习出来的模型适用于新样本的能力为:泛化能力(generalization),即从特殊到一般。
西瓜的例子中,我们是想计算机通过学习西瓜的特征数据,训练出一个决策模型,来判断一个新的西瓜是否是好瓜。可以得知我们预测的是:西瓜是好是坏,即好瓜与差瓜两种,是离散值。同样地,也有通过历年的人口数据,来预测未来的人口数量,人口数量则是连续值。定义:
- 预测值为离散值的问题为:分类(classification)。
- 预测值为连续值的问题为:回归(regression)。
我们预测西瓜是否是好瓜的过程中,很明显对于训练集中的西瓜,我们事先已经知道了该瓜是否是好瓜,学习器通过学习这些好瓜或差瓜的特征,从而总结出规律,即训练集中的西瓜我们都做了标记,称为标记信息。但也有没有标记信息的情形,例如:我们想将一堆西瓜根据特征分成两个小堆,使得某一堆的西瓜尽可能相似,即都是好瓜或差瓜,对于这种问题,我们事先并不知道西瓜的好坏,样本没有标记信息。定义:
- 训练数据有标记信息的学习任务为:监督学习(supervised learning),容易知道上面所描述的分类和回归都是监督学习的范畴。
训练数据没有标记信息的学习任务为:无监督学习(unsupervised learning),常见的有聚类(clustering)和关联规则。
训练training、验证validation/develop、测试testing 的作用
学得模型后,使用其进行预测的过程称为测试。
为什么要将数据集划分为三个部分?三个部分的作用?三个部分数据集的比例应如何设定?
另外一种常见的数据集划分方法是将数据集划分为两个部分(训练集和测试集),这种划分方法存在的问题在于,模型利用训练集数据进行训练,测试集数据进行模型泛化性测试。但我们不能利用测试集测试的bad case或者根据测试集的测试精度调整模型的参数。这是因为对于模型来说,数据集应该是只有训练集可见的,其他数据均不可见,如果利用测试集的结果调整模型相对于模型也”看到了“测试集的数据。将数据集划分为是独立同分布的三个部分就可以解决这个问题,将训练集数据用于模型训练,验证集(开发集)数据用于模型调参,测试集数据用于验证模型泛化性。
1.3 假设空间
归纳induction和演绎deduction
- 归纳:从特殊到一般的“泛化”过程,从具体事实归结一般规律。
演绎:从一般到特殊的“特化”过程,从基础原理推演具体情况。
假设hypothesis space、版本空间hypothesis space
假设空间:监督学习(supervised learning)的任务是学习一个模型,使模型能够对任意给定的输入,对其相应的输出做出 一个好的预测。模型属于由输入空间到输出空间的映射的集合,这个集合就是假设空间(hypothesis space)。我们也可以将学习过程看作一个在所有假设组成的空间中进行搜索的过程,搜索目标是找到与训练集”匹配”的假设,即能够将训练集中的瓜判断正确的假设。假设的表示一旦确定,假设空间及其规模大小就确定了。
版本空间:与训练集一致的“假设集合”。
1.4、归纳偏好inductive bias
在学习过程中对某种类型假设的偏好。有效的机器学习算法必有其归纳偏好。基于某种领域的知识而产生的归纳偏好,与特征选择不同,特征选择是基于训练样本分析选择有效的特征或者更加重视某类特征。
归纳偏好与问题本身匹配,偏好什么能让模型更好。 “奥卡姆剃刀”(Occam’s razor)是一种常用的、自然科学研究中最基本的原则,用于确立”正确的”偏好——即”若有多个假设与观察一致,则选最简单的那个“。
没有免费午餐定理No Free Lunch Theorem -NFL
根据奥卡姆剃刀原则,下图(a)中A曲线的泛化能力要比曲线B强,但可能存在图(b)这样的情况,B曲线更好地满足测试集样本。也就是说,针对某种分布的样本空间(某种问题),算法A可能优于B,而针对另外一种分布的样本空间(另外一种问题),算法B可能优于A,这就引出了没有免费午餐定理。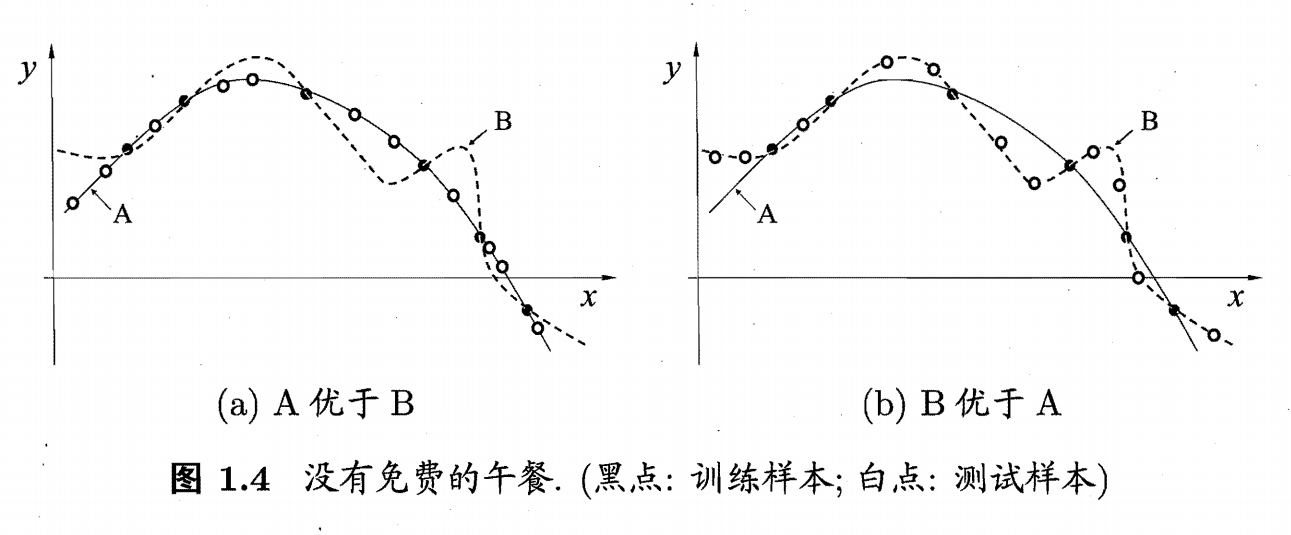
没有免费午餐定理表明:若考虑所有潜在的问题,所有学习算法的误差期望相同,也就是所有算法都一样好。因此,脱离具体问题空谈什么学习算法更好没有意义,在某些问题上表现好的学习算法在另外一些问题上可能不尽人意。学习算法自身的归纳偏好与目标问题是否匹配往往起决定作用。


